Results
The end of game results highlight the optimal allocation of each type of sushi and how frequently your students followed the optimal decision rule.

First, we present a table (Figure 1) which displays the percentage of students who maximized their utility (indicated here by the column % Answering Correctly).

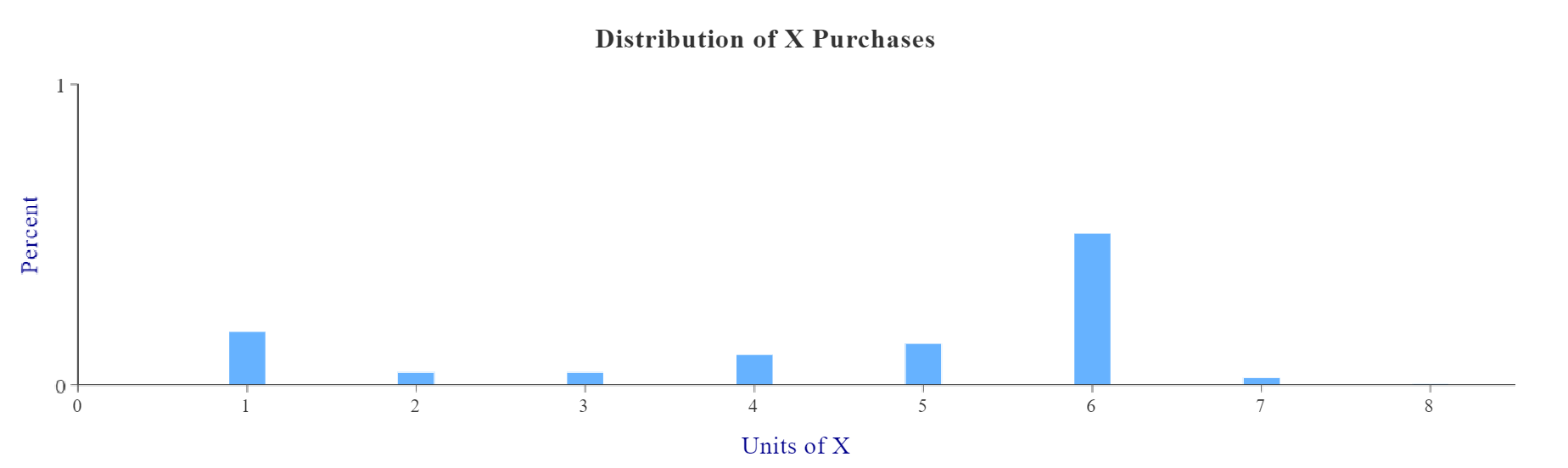
In the "Per-problem Details" section we show a summary table of each problem (Figure 2) and their optimal allocation of goods based on budget constraints. We then present a chart (Figure 3), showing how purchases of Good X are distributed in each problem. Click the radio buttons to toggle which problem is shown in the distribution chart.
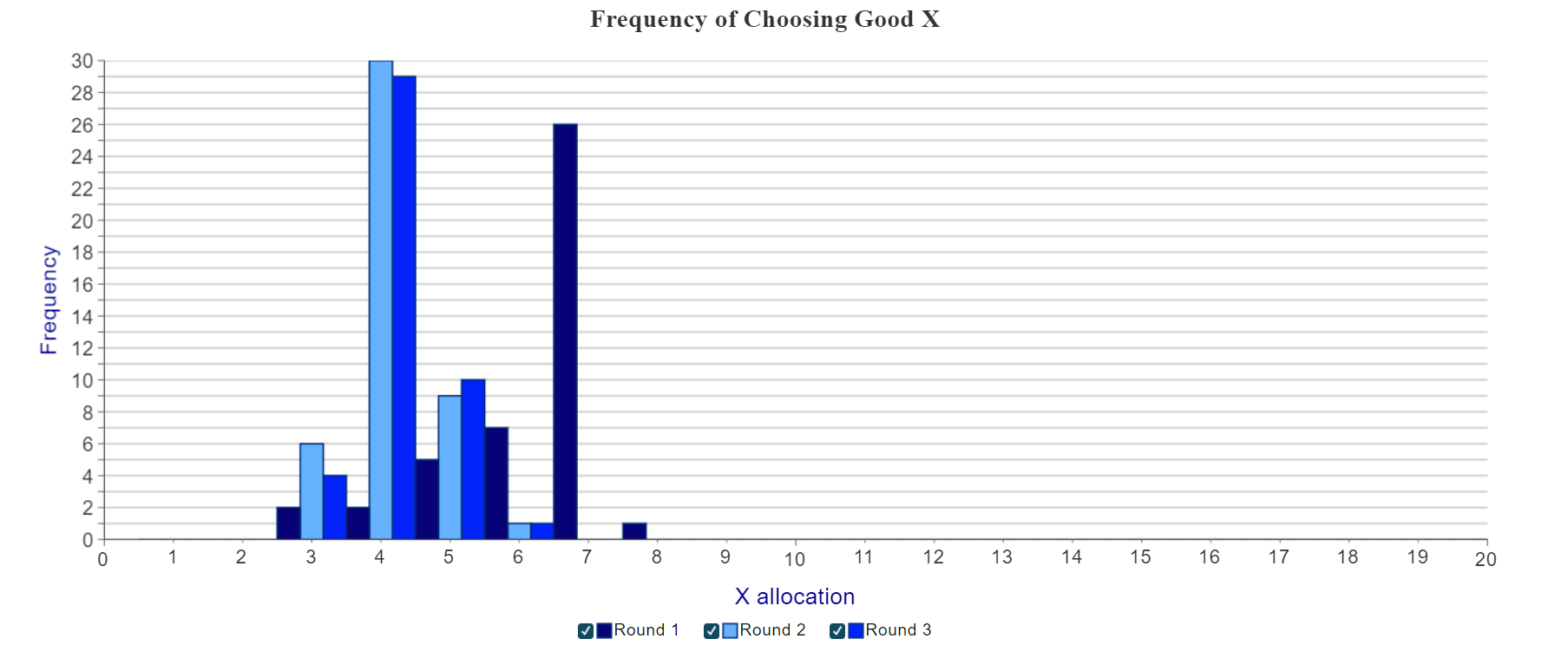
Next, we present a graph showing the frequency of choices of Good X across all rounds played (Figure 4).
Note that you can choose which round(s) to include in the graph. Simply click on the checkbox next to each item in the legend.
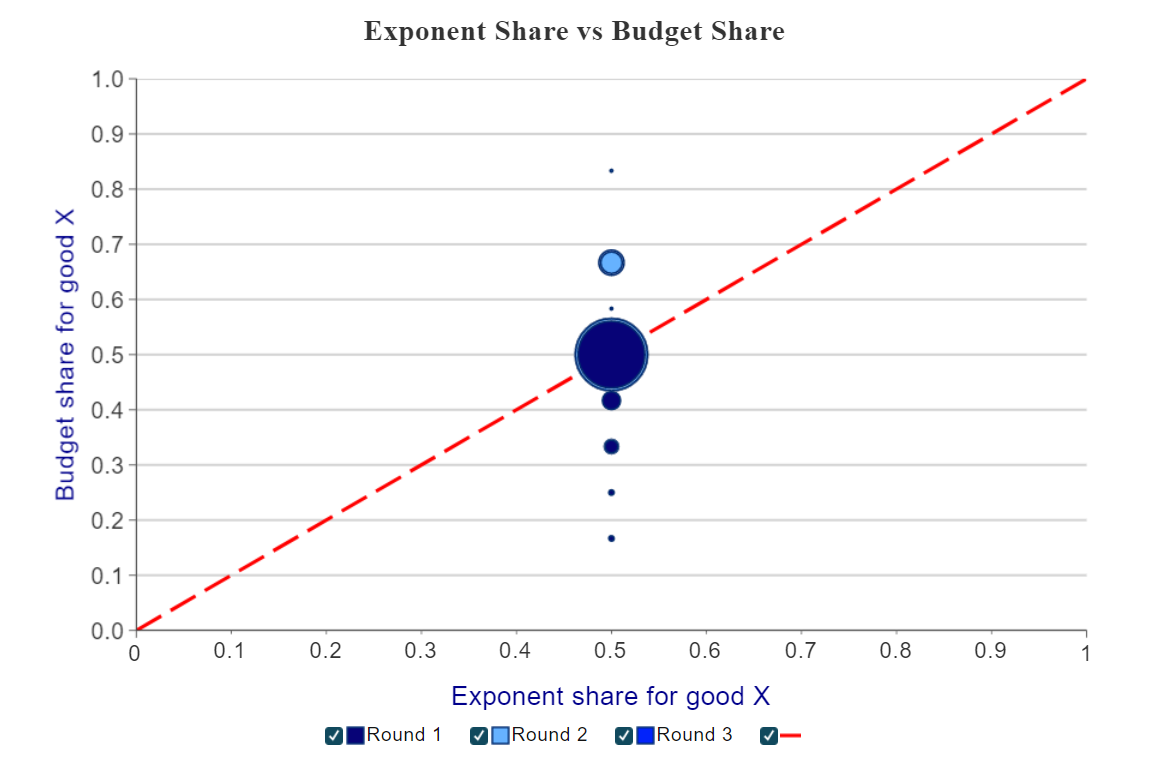
Finally, we present a graph (Figure 5) showing the relationship between the exponent and budget share for Good X across rounds. A shaded circle is displayed for each round, with larger circles indicating a greater number of observations. When a student is maximizing her utility, her budget share of Good X will be equal to her exponent share of Good X (shown by the dashed red line).
Note: Because this is a single player game, there are no robot strategies.
