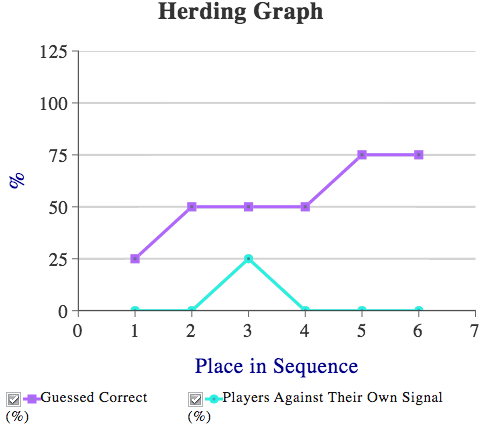
Because the final student in a game does not make his choice until all others have done so, you want to limit group size. To alleviate student wait time while still allowing the development of information cascades, we suggest Group Size of either 5 or 6.
The fraction of balls that are the majority color (% of Majority) is the primary parameter you can adjust. As discussed in the Equilibrium section, if players follow their own signal
when indifferent, a rational information cascade occurs the first time two balls of the same color are drawn sequentially, and it occurs on the incorrect choice when they are the minority color. Thus, increasing from the default of 60%, increases
the likelihood of a cascade, while reducing the likelihood of an incorrect one.
We recommend a few repetitions in order to facilitate learning. With Periods > 1 , a player maintains both his group and his order within that group across periods. By replaying a one-period game, you can ensure that
students play in different roles.
Finally, you may choose to run this game outside of the classroom. Choose how long the game will be available to students in the Duration panel, and check All Play Only Robots to have each
player grouped with automated players. We describe their strategies in the Robot Play section.
Summary
Assuming a student does not follow her private signal whenever her private signal leaves her indifferent between her two choices, then an information cascade occurs immediately. All students make the same choice as the student choosing
first. Assuming a student follows her private signal whenever indifferent, then an information cascade occurs after the same color ball is drawn twice in a row.
Notation:
We use \(\alpha\) for the fraction of balls that are the majority color (% of Majority). We use upper-case letters for choices and lower case for the ball drawn by a player. Thus \(R_2\) means player
2 guessed that the jar contained mostly red balls and \(b_2\) means she drew a blue one. Finally, \(Pr_i[J=B|\cdot]\) is player \(i\)’s conditional belief that the jar contains mostly blue balls.
Analysis Summary:
Each player uses Bayes’ Rule to update her beliefs and guesses that the jar contains mostly a color if the calculated likelihood that it contains mostly that color exceeds 50%.
Assume player 1 draws blue. As \(Pr_1[J=B|b_1]=\alpha\), she chooses Blue.
Assume player 2 also draws blue. By Bayes’ Rule, $$Pr_2[J=B|B_1,b_2]=\frac{\alpha^2}{\alpha^2+(1-\alpha)(1-\alpha)}>\frac{1}{2},$$ so unsurprisingly player 2 guesses blue. Note that anytime the public belief starts at \(\frac{1}{2}\) and
two blues are sequentially drawn, this will be the posterior belief of the person drawing the second blue.
Things get more interesting if player 2 draws a different color than 1, as \(Pr_2[J=B|B_1,r_2]=\frac{1}{2}\). We consider two cases. First, let us assume that whenever indifferent, a player joins the herd and chooses what her predecessor did (as opposed
to following her private signal). Because a player makes the same choice regardless of her private signal, the public belief remains unchanged at \(\alpha\). In other words, a herd always starts with player 1! (This is an information cascade because
after player 1’s choice, no subsequent private signals affect choices.)
We now assume the other extreme: whenever indifferent, a player is a contrarian and makes the opposite choice of his predecessor (that is, he follows his private signal when indifferent). Under this assumption, we consider player 3’s beliefs
after after each of player 2’s potential guesses.
First, if player 2 makes a different choice than player 1, we have \(Pr_3[J=B|B_1,R_2]=\frac{1}{2}\). That is, we know that player 1 drew red and player 2 drew blue, and this information favors neither being the majority.
Second, if player 2 makes the same choice as player 1 (but would have made the opposite choice if he drew the other color), as above we have \(Pr_3[J=B|B_1,B_2]=\frac{\alpha^2}{\alpha^2+(1-\alpha)(1-\alpha)}\). If player 3 now draws red, we have $$Pr_3[J=B|B_1,B_2,r3]=\frac{(1-\alpha)\frac{\alpha^2}{\alpha^2+(1-\alpha)(1-\alpha)}}{(1-\alpha)\frac{\alpha^2}{\alpha^2+(1-\alpha)(1-\alpha)}+\alpha(1-\frac{\alpha^2}{\alpha^2+(1-\alpha)(1-\alpha)})}=\alpha>\frac{1}{2}.$$
Therefore, even assuming players follow their own signal if indifferent, an information cascase occurs after two consecutive players make the same choice.
Interpretation:
While information cascades are likely even if players refuse to join the herd when indifferent, comparing the above cases provides insights into the potential inefficiency when trying to make inferences from the choices, as
opposed to information, of others.
When players follow the herd when indifferent, the indifferent player provides no information about his private signal and the resulting herd is based on a single signal. If players instead reverse the herd, a player reveals her private information
(delaying the onset of the herd) and any resulting herd will be based on stronger information (as two consecutive of the same color are needed).
To quantify the value of contrarians, consider the equilibrium likelihood that player 5 chooses incorrectly. When the majority color makes up 60% of the jar, without contrarians player 5 chooses incorrectly 40% of the time compared to approximately
32% with contrarians. With \(\alpha=80%\), the likelihood falls only to 20% without contrarians, but all the way to 8% with contrarians.